Good morning gamers,
We've posted a few articles from a guest author named Sharbie who's taken up writing on his own blog - and his stuff is good (you should check it out). Sharbie had a set of two articles written earlier in the year that talked about the Cave Drake: the first covered how good he is in combat, while the other covered some additional maths based on comments that were made (including one of my comments, I'm proud to say). My question was based on a scenario he provided about how someone like Elrond would fare against the Cave Drake in a one-on-one contest. Ignoring how likely you are of getting a one-on-one duel against a Cave Drake with Elrond (he's going to have bodyguards - or he should), let's assume that Elrond does find himself alone in that kind of fight? How do we figure out how likely either side is to win?
The answer to that question (the math behind it) is the topic for today: if I know how many dice I'm rolling and the Fight Value of my models, how can I build my own spreadsheet to figure out the answers to the questions I want to ask? Assuming you want to use Microsoft Excel (or a Google Spreadsheet or some other similar spreadsheet tool) and you want to learn how to fish (so to speak), read on.
Before we dig in, I must add that Rythbryt did a post on some of this a while back in his series on Heroic Strike - if you want to check your math results in this post against something right, you can look there to compare. We'll give examples to illustrate, but check against those if you don't believe me. Today we will be less concerned about explaining the numbers (though we will) as we are how to compute the numbers from a mathematically sound perspective.
Part 1: Finding Discrete Probabilities
We're going to begin by showing the "discrete probabilities" (statistical speak for "all the possible cases") that we would see if a Warrior of Minas Tirith were fighting a Morannon Orc: each has 1 Attack at Fight 3 and that translates into one six-sided die for each of them. The 6x6 grid would look like this:
Notice that the table we have has either a "V", an "H", or a "T" in them - this indicates whether the Warrior of Minas Tirith has the high roll ("V" for vertical), the Orc has the high roll ("H" for horizontal), or the roll is tied ("T" for tied). Even if we were computing a Ranger of Gondor against a Morannon Orc (where the F4 on the Ranger of Gondor means he wins ties), we'd still want to label the ties as "T" (since how we handle ties is dependent on the Fight Values and whether Elven-made weapons are in play). Since both of these can be variables in our inputs, we're not going to pre-determine them here.
Note: when making a tool of any kind, making things configurable is better than hard-wiring things.
Notice on the right I have a simple list of things that might affect our dueling roll - number of dice being rolled, the Fight Value of the model, whether it has an Elven-made weapon, and if there is a dueling penalty (options are "No", "-1", or "-2"). I color-code my boxes for the input type (orange is free-form typing, blue is a drop-down menu, which you can find if you go to "Data" >> "Data Validation") and I've selected the relevant options for each model - currently, none of this is doing anything, but we're laying ground-work, right?
We could count the boxes in the grid that are "V" to find out how often the Warrior of Minas Tirith beats the Morannon Orc straight-up (15/36), count the boxes with an "H" to find out how often the Morannon Orc beats the Warrior of Minas Tirith straight-up (15/36), and we can equally divide the number of times they tie, since they have the same Fight Value (3/36 each). That results in each side getting 18/36, or a 50% chance each of winning the duel. We knew this intuitively, but now you see in laid out.
Now let's do something harder: what happens when you have two Attacks on one model (or two models working together)? We'll change the Scenario from a Warrior of Minas Tirith fighting a Morannon Orc to an Iron Guard with a weapon-swapped axe fighting two Morannon Orcs (one with shield and one with spear) - same cost, 2 Attacks on each side. Can we still use the same 6x6 grid we used before? Why yes, yes we can - here's how . . .
Part 2: Computing Max Probability
If we take a 6x6 grid, we can visualize how two dice working together get a maximum value - consider the following 6x6 grid:
The colored boxes show us a few things - if an Iron Guard rolls two dice:
- 11/36 boxes fall in either a row or a column that gets a 6, so 11/36 rolls will result in the Iron Guard getting a 6 as his highest roll (which we'll refer to in this post as a "6-high").
- He'll get a 5-high in 9/36 trials;
- He'll get a 4-high in 7/36 trials;
- He'll get a 3-high in 5/36 trails;
- He'll get a 2-high in 3/36 trials; and
- He'll get a 1-high ("snake-eyes") in 1/36 trials.
In this second case, each side has the same discrete cases for getting a 6, a 5, a 4, etc., but for each of the 36 grid squares that are formed, we can find how likely each of those is to happen by multiplying the probabilities that each side gets those rolls. To get these values, I just entered in "=1/36" next to the 1, "=3/36" next to the 2, and so forth, using the 1/3/5/7/9/11-out-of-36 values we found above.
Note: remember how we said hard-coding values is not a good strategy? We'll fix the "=1/36" thing in a minute.
With these values now on the sides, we can compute the likelihood that each wins as follows:
In this summary table, we can use a SUMIF function to add all of the values that went in favor of the Iron Guard when the Morannon Orc rolled a 1 (in this particular spreadsheet, we can get this by filling cell D11 with the equation =SUMIF(D$4:D$9,$C11,$B$4:$B$9)*D$2, with the "$" locking rows/columns that they appear before, so we can copy this formula around and not accidentally change our inputs.
We can copy these cells to the right to find the Iron Guard's probabilities of winning straight-up. Then we can copy down the same formulas (their rows are locked, so we're still looking at the right stuff) and look for "H" instead of "V" - this will be all of the cumulative probabilities of the Morannon Orcs winning:
Finally, we copy down the formulas one more time and look for "T" instead of "H" or "V" - this will be the cumulative probability of tying fights:
Before we compute our final probability of success, we can compute how our Ties worked out: since we have Fight Value as an input, we can compare them and assign the ties to whoever has the highest Fight Value. If there is tied Fight Value, we can have Elven-made weapons (yes/no) as an input as well, which will help us figure out if there is a 50/50 split or a 33/67 split in tied results. Whatever our split for ties is, we can then add it to the previous probabilities of winning and come up with an answer:
So an Iron Guard with a weapon-swapped axe has a 61% chance of winning the fight against two Morannon Orcs (because he wins all of the ties and all of the instances when his highest die roll beats the Morannons). Learn something yet? Well, now we're going to tackle the last part we need to make this work for most of your projects - how to scale it beyond two-dice calculations . . .
Part 3: Linear Scaling
Okay, so now we know how to brute-force compute the probabilities of getting a 6-high, 5-high, 4-high, etc. on 1-2 dice - that's good, but not THAT useful for most of our computations. What happens when my 36 discrete probabilities increases when I roll three dice? Or four dice? And what happens if I'm trying to evaluate the effectiveness of the Watcher in the Water's SIX Attack dice (seven if he charges while in water)? I think we need a better solution.
Thankfully, we can turn to math - because math has been around since forever (as it happens) and when something has been around since forever and people have been paid for a long time to do math, they figure stuff out for you. Living in the Information Age means we can learn a lot from other people quickly, so that's what we'll do here.
We know that there are 6 discrete probabilities when we roll 1 die, 36 discrete probabilities when we roll 2 dice, 216 discrete probabilities when we roll 3 dice, etc. How do we get these numbers? The answer is exponents: 6^1 (or 6) is 6, 6^2 (or 6x6) is 36, 6^3 (or 6x6x6) is 216, and 6^4 (or 6x6x6x6) is 1296 - we can take the number 6 and raise it to the number of dice that we're rolling and that will tell us our total number of discrete cases that result from rolling that many dice.
Okay, so how did we turn our ability to get a 6-high or 5-high with two dice as a formula? We saw in our grid that our likelihood of getting a 1-high with two dice was 1/36 - and it turns out that our likelihood of getting a 1-high will always be "=1/(6^<number_of_dice>)". On the other side of the spectrum, our likelihood of getting a 6-high is 11/36 which happens to be "=1-((5/6)^<number_of_dice>)." This is basically "the times when you don't get a 1-5 on each dice."
Once we know the likelihood of getting a 6-high, we can find our chances of getting a 5-high by doing "=1-((2/3)^<number_of_dice>)-<pct_six_high>" (or basically "the times we didn't get a 1-4, subtracting the times we know we got a 6"). We can keep doing this for 4s ("=1-((1/2)^<number_of_dice>)-<pct_six_or_five_high>"), 3s ("=1-((1/3)^<number_of_dice>)-<pct_six_five_or_four_high>"), and 2s ("=1-((1/6)^<number_of_dice>)-<pct_six_five_four_or_three_high>") as well.
When we do this (using a more formulaic approach to finding the "5/6" and "2/3" values), we can make a lookup table for our percentages like this:
By copying this to the right, we can get the values easily for additional numbers of dice:
For those who aren't sure if these answers are right, you can follow my formulas and select all of the cells in a column and your answer will be 1 - which means all of the probabilities together add up to 100% (if percentages were a proper unit of measure for probabilities - colloquially we use them, but technically we shouldn't). You know what the best thing is about this? If you have an input for the number of dice (as we do in this spreadsheet), you can make this go up as high as you want just by adding more columns and copying your values to the right!
The last thing we need to do is change our hand-made lookups on the edges of the table to lookup their values from the newly-computed table of probabilities:
Now we're in a good place - do the same kind of lookup for the top row and you're good to go (if there aren't any two-handed weapons, unarmed models, or other weird situations)!
Part 4: Modifiers
The simplest modifier you'll need to compute is the -1 penalty that can be applied by two-handed weapons, unarmed models, banner-carriers, and pikemen carrying too many things. When this happens, you just need to change the max values that they're assigned to (6 becomes 5, 5 becomes 4, etc.). We can do that with a fairly complicated lookup on our probability VLOOKUP cells OR we can make custom cells for our "1" cells, our "6" cells, and then standard lookups for our 2-5 cells. The 1s look like this (if we have a -2 penalty, add the values for 1-3 - since all three result in a 1 being rolled, then if we have a -1 penalty, add the values for 1-2, and if neither is the case, return the result for 1):
You can run a similar formula for 6s (returning 0 for -2 or -1 penalties, looking up the normal result in other cases):
We've already covered a special case here - what happens when you have a -2 penalty (like you might get from an Uruk-Hai Warrior with a pike, shield, and banner) - the 5s cell needs a similar lookup to the 6s, where it scores a 0 if you have a -2 penalty, looks up a 6 if you get a -1 penalty, and then returns the normal lookup otherwise). All of the other cells (2-4) return the score for "<number>+1" when there is a -1 penalty applied and "<number>+2" when there is a -2 penalty applied. Pretty straight-forward, not going to illustrate it here.
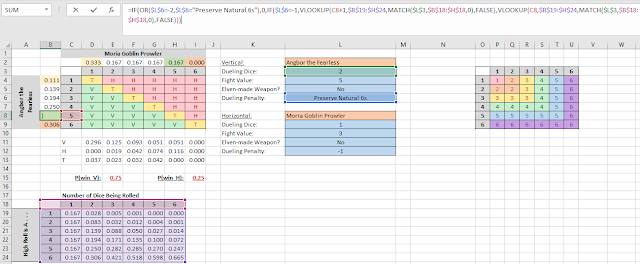
Another special case to consider is where natural 6s don't suffer a penalty (like Angbor the Fearless's Broadsword). This requires a modification to your Data Validation choice and some updates for each of your computations for 1-5 (6s get what they normally get):
There's one situation we can't handle with this table: getting +1 to your Dueling roll (which can happen in some Battle Companies and when you spend Might to boost a Dueling roll). We could add it to the dueling penalty box (as an alternative to getting -1 or -2 to your dueling roll), but there are many heroes who can suffer the -1 penalty to use a two-handed weapon AND might choose to boost their dueling roll, so we really need a separate box that accepts an input for how many pips we're willing to boost our roll by.
Computing this is actually . . . quite difficult. :) If you want to learn how to do it, keep watching this space - we'll address it next week. Hope you learned something - if there are other things you'd like to see, let us know in the comments. Until next time, happy hobbying!












So are two attacks with a double handed weapon at f4 better than one attack with an elven weapon at f5?
ReplyDeleteJust...
I think I've just bought a horde of hunter orcs and think if I give them all double handed picks, and piercing strike all the time, then it could be quite crazy.
A 2A Hunter Orc with a two-handed weapon has a probability of 0.417 of winning a duel against a 1A High Elf Warrior. This means that if you have five fights going on, you'll win two of them and lose three of them. If you used Piercing Strike (only necessary if the Elf was D5), you would would the 2 Elves you beat on a 3+ with each dice, which gives each warrior a 0.89 probability of killing his target (chances are good that they're both dead). In return, if we assume that the Defense of your troops in the remaining three fights drops to D3, D2, and D1, the D2/D3 guys will be wounded on 4s (expect one of them to die) and the D1 guy will be wounded on 3s (he might die).
DeleteAll told, you're looking at possibly two models from each side dying . . . so if you have the numerical advantage, this could be a winning strategy. :) I will add that by having a banner nearby (3 dice to win the fight), your Hunter Orcs each have a 0.494 probability of winning the fight (you're now winning half of the fights you win) and once again, you're killing almost all the Elves you fight. Even against D6 Elves, you have a 0.75 probability of killing them without the Piercing Strike. So . . . two-handed weapons for the win (makes me want to try two-handing more with Uruk-Hai Berserkers).
I absolutely love this! I've been looking for something like this. Thank you for the lesson in SBG, probability, and Excel.
ReplyDeleteI have a question:
Where are you hiding your lists for Data Validation is Part 1?
Oh, guess I didn't show that. :-) For this initial stage, I entered the values directly into the Data Validation pane instead of using cells. In our next article, you'll see that I put the stuff for data validation below row 24 so it would stay out of the way of the probability table. Each option has an associated die penalty with it (-1 or -2), so this gives us a two column table for looking up values.
Delete